Neural Word Embedding as Implicit Matrix Factorization

前言

尽管嵌入模型很明显是基于分布假设来进行优化，使常出现的word-context对向量内积极大化，并极小化随机word-context对内积。但对于这些优化指标的讨论很少，也不清楚为什么这样能够得到期望的结果。这篇文章对此进行了探讨，表明SGNS(skip-gram with negative-sampling)的训练方法实际上是加权矩阵分解，其目标函数在隐式地分解一个移动PMI矩阵，并基于此提出了更高效的优化方式。

SGNS

关于skip-gram with negative-sampling，这里就不再赘述，请查看下面两篇文章：

总的来说，SGNS的目标函数如下： \[ l=\Sigma_{w\in V_W}\Sigma_{c\in V_C}|(w,c)|(log\sigma(\vec{w}\cdot\vec{c})+k\cdot\mathbb{E}_{c_N\sim P_D}[log\sigma(-\vec{w}\cdot\vec{c}_N)])\tag{1} \] 这里\(V_W\)为单词集，\(V_C\)为上下文集，\(P_D\)为均匀测度满足\(P_D(c)=\frac{|(c)|}{|D|}\).

隐式矩阵分解下的SGNS

SGNS将单词以及上下文嵌入为低维空间的向量，得到单词与上下文向量构成的矩阵\(W\)与\(C\)，这两者实际上是相同的。\(W\)的行元素（即单词嵌入向量）被直接提取使用，但原始SG模型会进行上下文预测，SGNS可以看作是对矩阵\(M=W\cdot C^T\)的分解。

对于\(M\)，其分量\(M_{i,j}\)对应了\(W_i,C_j\)的向量积，这表示着特定单词与上下文的关联强度，而这种关联矩阵常常出现于NLP的研究中，但该矩阵并没有显式出现在SGNS的优化函数中，那么将SNGS看作对\(M\)的隐式分解说得通吗？如果不是，SGNS分解的是哪个矩阵呢？

刻画该隐式矩阵

重写式子\((1)\): \[ \begin{aligned} l&=\Sigma_{w\in V_W}\Sigma_{c\in V_C}|(w,c)|(log\sigma(\vec{w}\cdot\vec{c}))+\Sigma_{w\in V_W}\Sigma_{c\in V_C}\|(w,c)|(k\cdot\mathbb{E}_{c_N\sim P_D}[log\sigma(-\vec{w}\cdot\vec{c}_N)])\\ &=\Sigma_{w\in V_W}\Sigma_{c\in V_C}|(w,c)|(log\sigma(\vec{w}\cdot\vec{c}))+\Sigma_{w\in V_W}|(w)|(k\cdot\mathbb{E}_{c_N\sim P_D}[log\sigma(-\vec{w}\cdot\vec{c}_N)]) \end{aligned}\tag{2} \] 然后显式地计算出期望项： \[ \begin{aligned} \mathbb{E}_{c_N\sim P_D}[log\sigma(-\vec{w}\cdot\vec{c}_N)]&=\Sigma_{c_N\in V_C }\frac{|(c_N)|}{|D|}log\sigma(-\vec{w}\cdot\vec{c}_N)\\ &=\frac{|(c)|}{|D|}log\sigma(-\vec{w}\cdot\vec{c})+\Sigma_{c_N\in V_C\setminus \{c \}}\frac{|(c_N)|}{|D|}log\sigma(-\vec{w}\cdot\vec{c}_N) \end{aligned}\tag{3} \] 结合两式并将\(l\)改写为局部形式： \[ l(w,c)=|(w,c)|log\sigma (\vec{w}\cdot \vec{c})+k\cdot |(w)|\cdot\frac{|(c)|}{|D|}log\sigma(-\vec{w}\cdot\vec{c})\tag{4} \] 定义\(x=\vec{w}\cdot \vec{c}\)，并对其求导： \[ \frac{\partial{l}}{\partial{x}}=|(w,c)|\cdot\sigma(-x)-k\cdot|(w)|\frac{|(c)|}{|D|}\sigma(x) \] 令其为零得到： \[ e^{2x}-(\frac{|(w,c)|}{k\cdot|(w)|\cdot\frac{|(c)|}{|D|}}-1)e^x-\frac{|(w,c)|}{k\cdot|(w)|\cdot\frac{|(c)|}{|D|}}=0 \] 我们可以直接给出显式解： \[ \vec{w}\cdot \vec{c}=log(\frac{|(w,c)|\cdot|D|}{|(w)|\cdot |(c)|})-logk\tag{5} \] 这里指出\(log(\frac{|(w,c)|\cdot|D|}{|(w)|\cdot |(c)|})\)即\((w,c)\)的PMI(pointwise mutual information)，PMI常见于nlp的研究中，可以进一步将上式写为： \[ M_{i,j}^{SGNS}=W_i\cdot C_j=\vec{w}_i\cdot\vec{c}_j=PMI(w_i,c_j)-logk\tag{6} \] SGNS实际上在分解上述的矩阵，当\(k=1\)即负采样率为1时，SGNS的目标函数其实在分解由单词与上下文构成的关联矩阵，并且关联强度由PMI给出，这里将其定义为PMI阵，\(M^{PMI}\). 当\(k\)变化时，对应的PMI阵会有所偏移，\(M^{PMIk}=M^{PMI}-logk\).

其它的嵌入算法也可以相应理解，如noise-contrastive estimation模型分解的矩阵为： \[ M_{i,j}^{NCE}=\vec{w}_i\cdot \vec{c}_j=log(\frac{|(w,c)|}{|(c)|})-logk=logP(w|c)-logk\tag{7} \]

PMI

PMI是信息理论中用于度量一对离散输出\(x,y\)的度量函数： \[ PMI(x,y) = log\frac{P(x,y)}{P(x)P(y)}\tag{8} \] 在进行词嵌入时，上面的概率完全是由计数来估计的： \[ PMI(w,c)=log\frac{|(w,c)|\cdot|D|}{|(w)|\cdot |(c)|}\tag{9} \]

上面所给的PMI估计并不是定义良好的，当不存在某个\((w,c)\)对时，对应的估计将为负无穷，一个修改方式是将负无穷的分量重整为0。但考虑PMI的语义，这并不合理，更好的做法是将负值全都置为零，这称为postive PMI(PPMI)： \[ PPMI(w,c)=\max(PMI(w,c),0)\tag{10} \]

词嵌入的其它选择

首先由前面的推导，很容易得到下面的shifted PPMI: \[ SPPMI_k(w,c)=\max (PMI(w,c)-logk,0)\tag{11} \]

谱降维：SVD over Shifted PPMI

如果将SGNS理解为矩阵分解，那么通常的矩阵分解也可以直接用于求解词嵌入，这里使用truncated SVD.

SVD将M分解为三个矩阵的乘积\(U\cdot \Sigma \cdot V^T\)，这里\(U\)和\(V\)是正交阵，\(\Sigma\)为奇异值构成的对角阵。令\(\Sigma_d\)为前\(d\)个奇异值构成的对角阵，\(U_d\)和\(V_d\)为从\(U,V\)对应列抽出的子阵。\(M_d=U_d\cdot \Sigma_d \cdot V_d^T\)为\(M\)的秩\(d\)最佳估计，即有\(M_d=\mathop{\arg\min}\limits_{Rank(M')=d}||M'-M||_2\)成立.

如果使用SVD，那么\(W=U_d \cdot \Sigma_d\)行间的向量积等于\(M_D\)行间的向量积，使用\(W\)足够作为\(M_D\)的低维稠密表示。在NLP的研究中，一个常见方法是对PPMI矩阵\(M^{PPMI}\)进行SVD分解，并使用\(W^{SVD}=U_d\cdot \Sigma_d\)以及\(C^{SVD}=V_D\)的行元素分别作为单词与上下文表示。但这种方法得到的结果在语义任务上总是达不到SGNS的性能。

对称SVD

如果直接使用SVD来分解，那么最终得到的单词、上下文嵌入阵会相当不同，仅\(C^{SVD}\)为正交的，SGNS方法相比显得更加对称，故而这里使用如下的分解： \[ W^{SVD_{1/2}}=U_D\cdot \sqrt{\Sigma_d}\quad C^{SVD_{1/2}}=V_d\cdot \sqrt{\Sigma_d}\tag{12} \] 尽管缺乏理论解释，但在实践中进行对称化后能得到更好的性能。

SVD versus SGNS

SVD不需要训练以及超参数的调整，对任何\(\{(w,c,|(w,c)|)\}\)形式的数据都可以使用，泛用性更高。

而SGNS可以更好地处理观察，未观察事件；除此之外， SGNS对不同\((w,c)\)对分配了不同权重，这对于SVD来说是相当困难的，对于非稀疏的矩阵SGNS拥有更高的分解效率。

一个有趣的想法是使用随机矩阵分解，作者将其放在未来工作中。

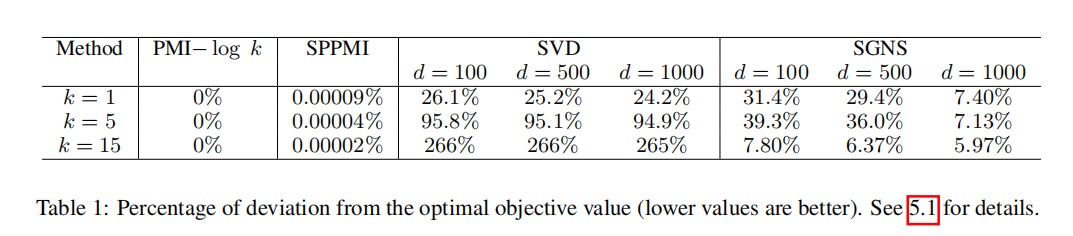
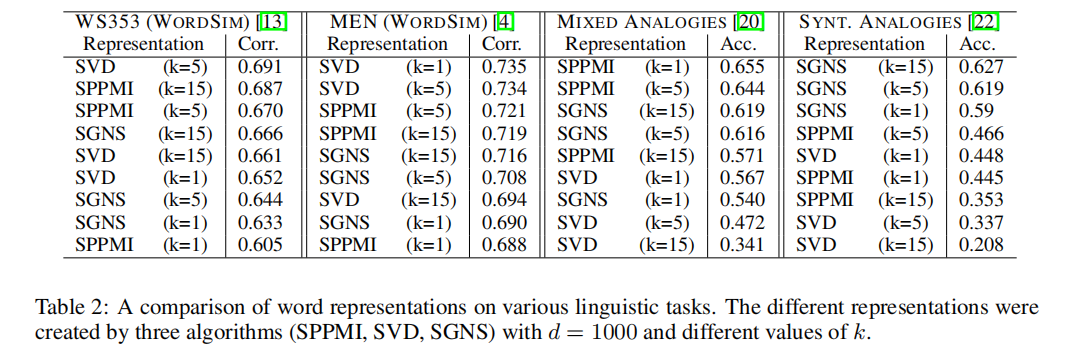
实验结果

个人觉得理论仍然不太充分，有些地方还是有点自圆其说，实验结果还过得去。